[통계] T 검정 (스튜던트 T-test) One Sample / Two Sample T-test

 

 

 

깃허브에서 코드보기

 

 

 

 

 

Student T-test¶

T- 검정은 모집단의 분산이나 표준편차를 알지 못할 때, 표본으로부터 추정된 분산이나 표준편차를 이용하여 두 모집단의 평균의 차이를 알아보는 검정 방법이다. 집단의 수는 최대 2개까지 비교 가능하며 3개 이상인 경우 분산분석(ANOVA)를 사용한다.

'평균'을 비교하는 분석임을 잊지말자.

 

T-검정의 가정

1)종속변수가 양적 변수일 때

2)모집단의 분산이나 표준편차를 알지 못할 때

3)모집단의 분포가 정규분포일 때

 

One Sample T-test¶

1개의 샘플(표본) 평균이 특정값(or 모집단)의 평균과 같은지/다른지를 판단

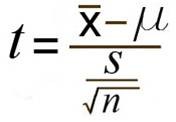
귀무가설: $\mu = \bar{X}$ 평균이 같다

대립가설: $\mu \neq \bar{X}$ X 같지 않다

(1) 귀무가설 설정 $H_0: \mu = \bar{x}$

(2) 대안가설 설정 $H_1: \mu \neq \bar{x}$

(3) 신뢰도 설정(Confidence Level) : 모수가 신뢰구간에 포함될 확률 (보통 95%)

모수가 신뢰 구간 안에 포함될 확률이 95%
귀무가설이 틀렸지만 우연히 성립할 확률이 5%

(4) P-value를 확인

P-value 는, 주어진 가설에 대해서 "얼마나 근거가 있는지"에 대한 값을 
0과 1사이의 값으로 scale한 지표 이며 
p-value가 낮다는 것은, 그 다름이 우연히 다를 가능성이 낮다는 것을 말한다.

" p-value가 (1-Confidence)보다 낮은 경우, 귀무가설을 기각하고 대안 가설을 채택함 "

 

1) t-value > Critical Value : 귀무가설 기각

2) p-value < alpha : 귀무가설 기각

In [4]:

from scipy import stats
import numpy as np

np.random.seed(42)
binomial_test = np.random.binomial(n = 1, p = 0.5, size = 100) 

binomial_test

Out[4]:

array([0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0,
       0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1,
       0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1,
       0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1,
       1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0])

In [8]:

binomial_test.mean()

Out[8]:

0.47

In [5]:

stats.ttest_1samp(binomial_test, .5) #0.5는 비교대상(혹은 모집단)의 평균

Out[5]:

Ttest_1sampResult(statistic=-0.5980699588110716, pvalue=0.5511590111236772)

 

0.47 (mean)과 0.5(mean)이 동일한지 확인하기
p-value가 0.05보다 크므로 귀무가설 채택. 둘의 평균은 같다고 볼 수 있다.

귀무가설 채택: $\mu = \bar{X}$

 

Two Sample T-test¶

위에서는 one sample 티테스트를 하였다면, 이제 2개의 sample 값들의 평균이 통계적으로 같은지, 다른지 확인해보겠습니다.

1) 귀무가설 : 두 확률은 같다 (차이가 없다).

$H_0: \bar{x}_1 = \bar{x}_2$

2) 대안가설 : 같지 않다

$H_1: \bar{x}_1 \neq \bar{x}_2$

3) 신뢰도 : 95%

 

확률을 p = 0.5로 두고 샘플링 하겠습니다.

In [10]:

np.random.seed(42)

sample1 = np.random.binomial(n = 1, p = 0.5, size = 100)
sample2 = np.random.binomial(n = 1, p = 0.5, size = 200)

print(sample1.mean())
print(sample2.mean())

stats.ttest_ind(sample1, sample2) # 둘의 평균은 같다.

 

0.47
0.545

Out[10]:

Ttest_indResult(statistic=-1.2247037746390195, pvalue=0.2216540739417425)

 

귀무가설 (둘의 평균이 다르지않다)가 채택되는 결과값이 나왔습니다.

 

이번에는 확률차이를 두고 샘플링을 해보겠습니다.

 

In [11]:

np.random.seed(42)

sample3 = np.random.binomial(n = 1, p = 0.7, size = 100)
sample4 = np.random.binomial(n = 1, p = 0.5, size = 200)

print(sample3.mean())
print(sample4.mean())

stats.ttest_ind(sample3, sample4) # 둘의 평균은 같지 않다

 

0.7
0.545

Out[11]:

Ttest_indResult(statistic=2.600202846578567, pvalue=0.00978123211440728)

 

결과 p-value가 0.05보다 작습니다. 이 경우 귀무가설을 기각하고, 대립가설: 둘의 평균은 같지 않다.가 채택됩니다.