[선형대수] 벡터의 내적, 전치행렬, 공분산, 상관계수

깃허브에서 코드보기

DamiSoh/Posting_Materials

 

 

 

 

 

 

벡터의 기본 개념 및 고교 수학 기록¶

 

벡터의 내적(Dot Product)¶

Terms Alert ! 곱, 내적, 정사영, Projection

벡터의 내적은 결과값이 스칼라로 표현됩니다.

우리가 익숙한 식은 다음과 같습니다.

$\vec{a}$와
$\vec{b}$ 에서 수선의 발을 내려 $\vec{a}$와 내적하는 부분을 곱해주는 것입니다. 그 길이는 |b|의 코사인 세타입니다.

 

 

또, 평면벡터일 때는 하기와 같이 계산합니다.

출처: 수악중독

 

선형대수에서 마주친 벡터가 너무 어려워, 고교 수학 공식을 가져다 쓰는 저의 비루함을 이해해주세요. 이렇게 보니 좀 시원한 감이 있지 않나요?

 

따라서 벡터 $\vec{v}$ 와 $\vec{x}$ 의 내적은 다음과 같이 계산해주시면 되겠습니다.

v = [1, 2, 3, 4]

x = [5, 6, 7, 8]

𝑣⃗ ⋅𝑥⃗ = 1 5 + 2 6 + 3 7 + 4 8

= 70

 

벡터의 내적은 다음과 같이 넘파이 np.dot(vector1, vector2)로 계산합니다

In [1]:

import numpy as np

v = np.array([1, 2, 3, 4])
x = np.array([5, 6, 7, 8])

np.dot(v, x)

Out[1]:

70

 

전치행렬(Transpose) : 행과 열을 바꾼 매트릭스를 말합니다¶

\begin{align} B^{T} \qquad B^{\prime} \end{align}

매트릭스에 .T로 진행합니다.

In [3]:

vector = np.array([[1,2,3,4], [5,6,7,8]])
vector

Out[3]:

array([[1, 2, 3, 4],
       [5, 6, 7, 8]])

In [4]:

vector.T

Out[4]: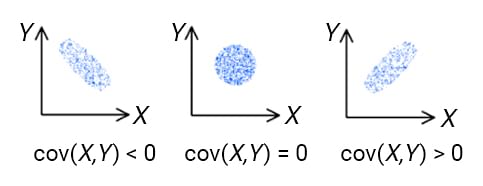

array([[1, 5],
       [2, 6],
       [3, 7],
       [4, 8]])

 

공분산 Covariance¶

한 개의 변수 값이 변화할 때 다른 변수가 어떤 연관을 가지고 변화하는지 측정하는 것입니다.

 

 

공분산이 음인 경우 변수 X,Y는 음의 상관관계를, 양인 경우에는 양의 상관관계를 가진다고 볼 수 있습니다.

In [10]:

import pandas as pd

df = pd.DataFrame([[170,60], [156,49], [165,52]], columns = ('키', '몸무게'))
df

Out[10]:

	키	몸무게
0	170	60
1	156	49
2	165	52

In [11]:

df.cov() #양의 상관관계를 가진다고 말할 수 있습니다.

Out[11]:

	키	몸무게
키	50.333333	36.833333
몸무게	36.833333	32.333333

 

상관계수 (Correlation Co-efficient)¶

위의 공분산은 그 데이터의 스케일에 따라 값이 달라지기 때문에, 비교하기 다소 어렵습니다. 상관계수는 그 범위를 -1 부터 1사이로 조정해줍니다

\begin{align} cor(X,Y) = r = \frac{cov(X,Y)}{\sigma_{X}\sigma_{Y}} \end{align}

In [12]:

df.corr()

Out[12]:

	키	몸무게
키	1.000000	0.913036
몸무게	0.913036	1.000000

In [ ]: